冒泡排序

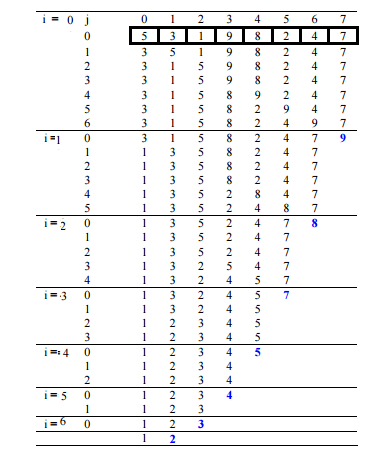
images

    public void sort(Integer[] arr){
        int length = arr.length;
        for(int i = 0;i<length;i++){
            for(int j = 0; j<length-i-1; j++){
                //交换位置
                if(arr[j] > arr[j+1]){
                    int temp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = temp;
                }
            }
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13

    public void optimizedSort(Integer[] arr){
        int length = arr.length;
        //交换标记
        boolean swapped;
        for(int i = 0;i<length;i++){
            //开始未发生交换
            swapped = false;
            for(int j = 0; j<length-i-1; j++){
                if(arr[j] > arr[j+1]){
                    int temp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = temp;
                    //设定交换标记为真
                    swapped = true;
                }
            }
            //如果没有发生交换，说明为有序数组，不再执行剩下的循环。
            if (swapped == false)
                break;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

插入排序

images

    //插入排序：
    //想想你手里有一些扑克牌，需要按照从小到大的顺序排序。
    //step 1 : 第二张牌与第一张牌比较，如果第二张牌小，则把第二张牌插在第一张前面
    //step 2 :第三张牌与第二张比较，如果第三张小则在与第一张牌比较，把小的插在大的前面，直到找完第一张牌。
    public void sort(Integer[] arr){
        int length = arr.length;
        for(int i = 1;i<length;i++){
            int num = arr[i];
            int j = i-1;
            while (j>=0 && arr[j] > num) {
                arr[j+1] = arr[j];
                j = j-1;
            }
            arr[j+1] = num;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

选择排序

images

    ///选择排序算法通过从未排序的部分重复查找最小元素（考虑升序）并将其放在开头来对数组进行排序。
    // 该算法在给定数组中维护两个子数组。
    //
    //1）已经排序的子数组。
    //2）未排序的剩余子数组。
    //
    //在选择排序的每次迭代中，挑选来自未排序子阵列的最小元素（考虑升序）并将其移动到排序子阵列。
    public void sort(Integer[] arr){
        int length = arr.length;
        //一开始未排序，设定最小的为数组第一个，然后依次与第一个比较
        for(int i = 0; i< length;i++){
            int min_idx = i;
            //找到最小的后，与第一个数交换位置,然后开始从第二个数重新找最小的
            for (int j = i+1; j < length; j++)
                if (arr[j] < arr[min_idx])
                    min_idx = j;
            int temp = arr[min_idx];
            arr[min_idx] = arr[i];
            arr[i] = temp;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

快速排序

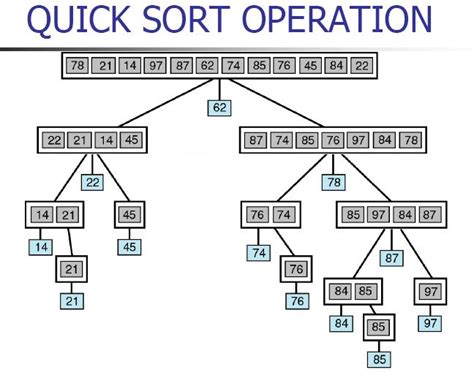
images

    //
    //First, we check the indices and continue only if there are still elements to be sorted.
    //We get the index of the sorted pivot and use it to recursively call partition() method
    // with the same parameters as the quickSort() method, but with different indices:
    public void sort(Integer arr[], int begin, int end) {
        if (begin < end) {
            int partitionIndex = partition(arr, begin, end);

            sort(arr, begin, partitionIndex-1);
            sort(arr, partitionIndex+1, end);
        }
    }

    // For simplicity, this function takes the last element as the pivot.
    // Then, checks each element and swaps it before the pivot if its value is smaller.
    //
    //By the end of the partitioning, all elements less then the pivot are on the left of it
    // and all elements greater then the pivot are on the right of it.
    // The pivot is at its final sorted position and the function returns this position:
    private int partition(Integer arr[], int begin, int end) {
        int pivot = arr[end];
        int i = (begin-1);// index of smaller element

        for (int j = begin; j < end; j++) {
            // If current element is smaller than or
            // equal to pivot
            if (arr[j] <= pivot) {
                i++;
                // swap arr[i] and arr[j]
                int swapTemp = arr[i];
                arr[i] = arr[j];
                arr[j] = swapTemp;
            }
        }
        // swap arr[i+1] and arr[high] (or pivot) 
        int swapTemp = arr[i+1];
        arr[i+1] = arr[end];
        arr[end] = swapTemp;

        return i+1;
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

Merge Sort

images

    public  void sort(Integer[] arr,int n){
        if (n < 2) {
            return;
        }
        int mid = n / 2;
        Integer[] l = new Integer[mid];
        Integer[] r = new Integer[n - mid];

        for (int i = 0; i < mid; i++) {
            l[i] = arr[i];
        }
        for (int i = mid; i < n; i++) {
            r[i - mid] = arr[i];
        }
        sort(l, mid);
        sort(r, n - mid);

        merge(arr, l, r, mid, n - mid);
    }

    public void merge(Integer[] a, Integer[] l, Integer[] r, int left, int right) {
            int i = 0, j = 0, k = 0;
            while (i < left && j < right) {
                if (l[i] <= r[j]) {
                    a[k++] = l[i++];
                }
                else {
                    a[k++] = r[j++];
                }
            }
            while (i < left) {
                a[k++] = l[i++];
            }
            while (j < right) {
                a[k++] = r[j++];
            }
    }
	```
## Heap Sort

Heap sort is a comparison based sorting technique based on Binary Heap data structure. It is similar to selection sort where we first find the maximum element and place the maximum element at the end. We repeat the same process for remaining element.

### What is Binary Heap?

Let us first define a Complete Binary Tree. A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible (Source Wikipedia)

A Binary Heap is a Complete Binary Tree where items are stored in a special order such that value in a parent node is greater(or smaller) than the values in its two children nodes. The former is called as max heap and the latter is called min heap. The heap can be represented by binary tree or array.

### Why array based representation for Binary Heap?
Since a Binary Heap is a Complete Binary Tree, it can be easily represented as array and array based representation is space efficient. If the parent node is stored at index I, the left child can be calculated by 2 * I + 1 and right child by 2 * I + 2 (assuming the indexing starts at 0).

### Heap Sort Algorithm for sorting in increasing order:

1. Build a max heap from the input data.
2. At this point, the largest item is stored at the root of the heap. Replace it with the last item of the heap followed by reducing the size of heap by 1. Finally, heapify the root of tree.
3. Repeat above steps while size of heap is greater than 1.

### How to build the heap?

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

Input data: 4, 10, 3, 5, 1 4(0) /
10(1) 3(2) /
5(3) 1(4)

The numbers in bracket represent the indices in the array representation of data.

Applying heapify procedure to index 1: 4(0) /
10(1) 3(2) /
5(3) 1(4)

Applying heapify procedure to index 0: 10(0) /
5(1) 3(2) /
4(3) 1(4) The heapify procedure calls itself recursively to build heap in top down manner.



```java
    public void sort(Integer arr[]) {
       int n = arr.length;

       // Build heap (rearrange array)
       for (int i = n / 2 - 1; i >= 0; i--)
           heapify(arr, n, i);

       // One by one extract an element from heap
       for (int i=n-1; i>=0; i--) {
           // Move current root to end
           int temp = arr[0];
           arr[0] = arr[i];
           arr[i] = temp;

           // call max heapify on the reduced heap
           heapify(arr, i, 0);
       }
   }

   // To heapify a subtree rooted with node i which is
   // an index in arr[]. n is size of heap
   void heapify(Integer arr[], int n, int i) {
       int largest = i; // Initialize largest as root
       int l = 2*i + 1; // left = 2*i + 1
       int r = 2*i + 2; // right = 2*i + 2

       // If left child is larger than root
       if (l < n && arr[l] > arr[largest])
           largest = l;

       // If right child is larger than largest so far
       if (r < n && arr[r] > arr[largest])
           largest = r;

       // If largest is not root
       if (largest != i) {
           int swap = arr[i];
           arr[i] = arr[largest];
           arr[largest] = swap;

           // Recursively heapify the affected sub-tree
           heapify(arr, n, largest);
       }
   }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

Sort in Java

Sort String

Internally, String uses an array of characters to operate on. Therefore, we can make use of the toCharArray() : char[] method, sort the array and create a new String based on the result:

@Test
void givenString_whenSort_thenSorted() {
    String abcd = "bdca";
    char[] chars = abcd.toCharArray();
 
    Arrays.sort(chars);
    String sorted = new String(chars);
 
    assertThat(sorted).isEqualTo("abcd");
}

1
2
3
4
5
6
7
8
9
10

In Java 8, we can leverage the Stream API to sort the String for us:

@Test
void givenString_whenSortJava8_thenSorted() {
    String sorted = "bdca".chars()
      .sorted()
      .collect(StringBuilder::new, StringBuilder::appendCodePoint, StringBuilder::append)
      .toString();
 
    assertThat(sorted).isEqualTo("abcd");
}

1
2
3
4
5
6
7
8
9

Sort ArrayList

@Before
public void initVariables () {
    toSort = new int[] 
      { 5, 1, 89, 255, 7, 88, 200, 123, 66 }; 
    sortedInts = new int[] 
      {1, 5, 7, 66, 88, 89, 123, 200, 255};
    sortedRangeInts = new int[] 
      {5, 1, 89, 7, 88, 200, 255, 123, 66};
    ...
}

1
2
3
4
5
6
7
8
9
10

sort complete array

@Test
public void givenIntArray_whenUsingSort_thenSortedArray() {
    Arrays.sort(toSort);
 
    assertTrue(Arrays.equals(toSort, sortedInts));
}

1
2
3
4
5
6

sort part of array


Arrays.sort(int[] a, int fromIndex, int toIndex)

@Test
public void givenIntArray_whenUsingRangeSort_thenRangeSortedArray() {
    Arrays.sort(toSort, 3, 7);
  
    assertTrue(Arrays.equals(toSort, sortedRangeInts));
}

1
2
3
4
5
6
7
8
9

Java 8 Arrays.parallelSort

@Test
public void givenIntArray_whenUsingParallelSort_thenArraySorted() {
    Arrays.parallelSort(toSort);
  
    assertTrue(Arrays.equals(toSort, sortedInts));
}

1
2
3
4
5
6

Sorting a List

@Test
public void givenList_whenUsingSort_thenSortedList() {
    List<Integer> toSortList = Ints.asList(toSort);
    Collections.sort(toSortList);
 
    assertTrue(Arrays.equals(toSortList.toArray(), 
    ArrayUtils.toObject(sortedInts)));
}

1
2
3
4
5
6
7
8

As mentioned in Oracle JavaDoc for Collections.Sort, it uses a modified mergesort and offers guaranteed n log(n) performance.

Sorting a Set

use Collections.sort() to sort a LinkedHashSet.

We’re using the LinkedHashSet because it maintains insertion order.

Notice how, in order to use the sort API in Collections – we’re first wrapping the set in a list:

@Test
public void givenSet_whenUsingSort_thenSortedSet() {
    Set<Integer> integersSet = new LinkedHashSet<>(Ints.asList(toSort));
    Set<Integer> descSortedIntegersSet = new LinkedHashSet<>(
      Arrays.asList(new Integer[] 
        {255, 200, 123, 89, 88, 66, 7, 5, 1}));
         
    List<Integer> list = new ArrayList<Integer>(integersSet);
    Collections.sort(list, (i1, i2) -> {
        return i2 - i1;
    });
    integersSet = new LinkedHashSet<>(list);
         
    assertTrue(Arrays.equals(
      integersSet.toArray(), descSortedIntegersSet.toArray()));

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

Sorting Custom Objects

Using Comparable

public class Employee implements Comparable {
    ...
 
    @Override
    public boolean equals(Object obj) {
        return ((Employee) obj).getName().equals(getName());
    }
 
    @Override
    public int compareTo(Object o) {
        Employee e = (Employee) o;
        return getName().compareTo(e.getName());
    }
}

@Test
public void givenEmpArray_SortEmpArray_thenSortedArrayinNaturalOrder() {
    Arrays.sort(employees);
 
    assertTrue(Arrays.equals(employees, employeesSorted));
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

Using Comparator

@Test
public void givenIntegerArray_whenUsingSort_thenSortedArray() {
    Integer [] integers = ArrayUtils.toObject(toSort);
    Arrays.sort(integers, new Comparator<Integer>() {
        @Override
        public int compare(Integer a, Integer b) {
            return a - b;
        }
    });
  
    assertTrue(Arrays.equals(integers, ArrayUtils.toObject(sortedInts)));
}

Arrays.sort(employees, new Comparator<Employee>() {
    @Override
    public int compare(Employee o1, Employee o2) {
       return (int) (o1.getSalary() - o2.getSalary());
    }
 });

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

Sort a HashMap

Using TreeMap

For starters, let’s define a HashMap and initialize it with some data:

Map<String, Employee> map = new HashMap<>();
 
Employee employee1 = new Employee(1L, "Mher");
map.put(employee1.getName(), employee1);
Employee employee2 = new Employee(22L, "Annie");
map.put(employee2.getName(), employee2);
Employee employee3 = new Employee(8L, "John");
map.put(employee3.getName(), employee3);
Employee employee4 = new Employee(2L, "George");
map.put(employee4.getName(), employee4);

1
2
3
4
5
6
7
8
9
10

For the Employee class, note that we’ve implemented Comparable:

public class Employee implements Comparable<Employee> {
 
    private Long id;
    private String name;
 
    // constructor, getters, setters
 
    // override equals and hashCode
    @Override
    public int compareTo(Employee employee) {
        return (int)(this.id - employee.getId());
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13

Next, we store the entries in the TreeMap by using its constructor:

TreeMap<String, Employee> sorted = new TreeMap<>(map);

Or, the putAll method to copy the data:

TreeMap<String, Employee> sorted = new TreeMap<>();
sorted.putAll(map);

1
2

And that’s it! To make sure our map entries are sorted by key, let’s print them out:

Annie=Employee{id=22, name='Annie'}
George=Employee{id=2, name='George'}
John=Employee{id=8, name='John'}
Mher=Employee{id=1, name='Mher'}

1
2
3
4

As we see, the keys are sorted in natural order.

Using ArrayList

#####Sort by Key

List<String> employeeByKey = new ArrayList<>(map.keySet());
Collections.sort(employeeByKey);

1
2

[Annie, George, John, Mher]

Sort by Value

First, let’s copy the values into the list:

List<Employee> employeeById = new ArrayList<>(map.values());

And after that, we sort it:

Collections.sort(employeeById);

print the employeeById:

[Employee{id=1, name='Mher'}, 
Employee{id=2, name='George'}, 
Employee{id=8, name='John'}, 
Employee{id=22, name='Annie'}]

1
2
3
4

Using a TreeSet

In case we don’t want to accept duplicate values in our sorted collection, there is a nice solution with TreeSet.

First, let’s add some duplicate entries to our initial map:

Employee employee5 = new Employee(1L, "Mher");
map.put(employee5.getName(), employee5);
Employee employee6 = new Employee(22L, "Annie");
map.put(employee6.getName(), employee6);

1
2
3
4

Sort by Key

To sort the map by its key entries:

SortedSet<String> keySet = new TreeSet<>(map.keySet());

Let’s print the keySet and see the output:

[Annie, George, John, Mher]

Now we have the map keys sorted without the duplicates.

Sort by Value

Likewise, for the map values, the conversion code looks like:

SortedSet<Employee> values = new TreeSet<>(map.values());

And the results are:

[Employee{id=1, name='Mher'}, 
Employee{id=2, name='George'}, 
Employee{id=8, name='John'}, 
Employee{id=22, name='Annie'}]

1
2
3
4

As we can see, there are no duplicates in the output. This works with custom objects when we override equals and hashCode.

Using Lambdas And Streams

Since the Java 8, we can use the Stream API and lambda expressions to sort the map. All we need is to call the sorted method over the map’s stream pipeline.

Sort by Key

To sort by key, we use the comparingByKey comparator:

map.entrySet()
  .stream()
  .sorted(Map.Entry.<String, Employee>comparingByKey())
  .forEach(System.out::println);

1
2
3
4

The final forEach stage prints out the results:

Annie=Employee{id=22, name='Annie'}
George=Employee{id=2, name='George'}
John=Employee{id=8, name='John'}
Mher=Employee{id=1, name='Mher'}

1
2
3
4

By default, the sorting mode is ascending.

Sort by Value

Of course, we can sort by the Employee objects as well:

map.entrySet()
  .stream()
  .sorted(Map.Entry.comparingByValue())
  .forEach(System.out::println);

1
2
3
4

As we see, the code above prints out a map sorted by the id fields of Employee objects:

Mher=Employee{id=1, name='Mher'}
George=Employee{id=2, name='George'}
John=Employee{id=8, name='John'}
Annie=Employee{id=22, name='Annie'}

1
2
3
4

Additionally, we can collect the results into a new map:

Map<String, Employee> result = map.entrySet()
  .stream()
  .sorted(Map.Entry.comparingByValue())
  .collect(Collectors.toMap(
    Map.Entry::getKey, 
    Map.Entry::getValue, 
    (oldValue, newValue) -> oldValue, LinkedHashMap::new));

1
2
3
4
5
6
7

Note that we collected our results into a LinkedHashMap. By default, Collectors.toMap returns a new HashMap, but as we know, HashMap doesn’t guarantee iteration order, while LinkedHashMap does.

Using Guava

Lastly, a library that allows us to sort the HashMap is Guava. Before we start, it’ll be useful to check our write-up about maps in Guava.

First, let’s declare an Ordering as we want to sort our map by Employee’s Id field:

Ordering naturalOrdering = Ordering.natural()
  .onResultOf(Functions.forMap(map, null));

1
2

Now, all we need is to use ImmutableSortedMap to illustrate the results:

ImmutableSortedMap.copyOf(map, naturalOrdering);

And once again, the output is a map ordered by the id field:

Mher=Employee{id=1, name='Mher'}
George=Employee{id=2, name='George'}
John=Employee{id=8, name='John'}
Annie=Employee{id=22, name='Annie'}

1
2
3
4

# 冒泡排序

# 插入排序

# 选择排序

# 快速排序

# Merge Sort

# Sort in Java

# Sort String

# Sort ArrayList

#

# sort complete array

# sort part of array

# Java 8 Arrays.parallelSort

# Sorting a List

# Sorting a Set

# Sorting Custom Objects

# Using Comparable

# Using Comparator

# Sort a HashMap

# Using TreeMap

# Using ArrayList

# Sort by Value

# Using a TreeSet

# Sort by Key

# Sort by Value

# Using Lambdas And Streams

# Sort by Key

# Sort by Value

# Using Guava

冒泡排序

插入排序

选择排序

快速排序

Merge Sort

Sort in Java

Sort String

Sort ArrayList

sort complete array

sort part of array

Java 8 Arrays.parallelSort

Sorting a List

Sorting a Set

Sorting Custom Objects

Using Comparable

Using Comparator

Sort a HashMap

Using TreeMap

Using ArrayList

Sort by Value

Using a TreeSet

Sort by Key

Sort by Value

Using Lambdas And Streams

Sort by Key

Sort by Value

Using Guava